Algoritmos Randomizados
Contenidos
Ejercicio resuelto
Solución
Ejercicios propuestos
-
(★★) Realizar un seguimiento al operar con una Skip List (inicialmente vacía) para agregar los siguientes elementos:
8, 12, 20, 15, 5, 2, 9, 14. Cuando se necesiten resultados aleatorios, se puede utilizar la siguiente secuencia:0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0. Luego mostrar un seguimiento de las búsquedas de: 18, 9 y 2. -
(★★) Explicar detalladamente por qué elegimos un pivote de forma aleatoria para Quicksort. ¿Cuál es la complejidad esperada para el algoritmo? Justificar (no es necesario entrar en demostraciones utilizando probabilidad y estadística, pero esperamos una noción) Sin saber nada de las posiciones que QuickSort va a elegir como pivote, ¿Cómo podría forzar el usuario que el algoritmo demore más tiempo que el esperado?
-
(★★★) Se tiene una función
monedaCargadaque devuelve 0 el 60% de las veces, y 1 el 40% de las veces. Implementar una función que utilice la antes mencionada, que devuelva 0 o 1 de forma aleatoria de forma equiprobable (es decir, con probabilidad 50/50). ¿Cuál es la complejidad esperada para el algoritmo? Justificar.Quiero una pista
Si ejecuto dos veces la función `monedaCargada`, ¿cuál es la probabilidad de que primero salga un 0 y luego un 1? ¿y la de que primero salga 1 y luego un 0? -
(★★★) Dado un Grafo, planteamos el siguiente algoritmo de aproximación randomizado para obtener el Independent Set más grande, para el caso de un grafo \(d\)-regular (es decir, un grafo en el cual todos los vértices tienen grado exactamente \(d\)): Para cada vértice \(v\) seleccionar de forma uniformemente aleatoria \(x_v\) el valor 0 o 1. Seleccionar para el Independent Set únicamente aquellos vértices con el valor 1 que no se conecten mediante aristas con otros vértices que tengan el valor 1.
a. Probar que el set resultante es independiente.
b. Calcula el tamaño esperado del set independiente (en función de \(n\) y \(d\)).
c. Para el cálculo de \(x_v\) utilizamos \(p = \frac{1}{2}\). Determinar si este es el valor mas conveniente o podemos encontrar uno mejor. Si es asi, de la fórmula del valor esperado con esta nueva probabilidad.
-
(★★★) Se tiene un polígono irregular que sabemos que encaja en un rectángulo de bas
By alturaH. Asumir que se cuenta con una funcióndentro_del_poligono(punto), que retornaTruesi el punto dado por parámetro esta dentro del polígono,Falseen caso contrario. Proponer un algoritmo randomizado con el que se pueda estimar el área de esta figura irregular.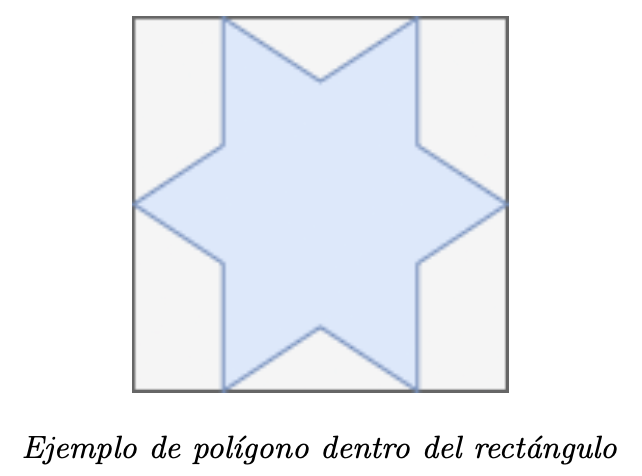
-
(★) Si le preguntamos a ChatGPT o Gemini qué es un algoritmo de tipo Sherwood (otro nombre para Las Vegas), Este nos responde con un texto similar a “The Sherwood algorithm, specifically in the context of binary search, is a randomized approach that introduces randomness to the selection of the middle element during each step. This contrast with the standard binary search algorithm, which always chooses the middle index based on
(first + last) / 2. The Sherwood algorithm usesfirst + rand.randInt(last - first + 1)to introduce randomness. This modification helps to mitigate the worst-case performance of binary search”.Explicar por qué podemos estar tranquilos y reirnos cuando nos dicen que la IA viene a reemplazar el trabajo de Ingenieros/as informáticos.