Trabajo Práctico n.º 1

Teoría de Algoritmos 1 - 2c 2024 Trabajo Práctico 1

Lineamientos básicos

El trabajo se realizará en grupos de cuatro o cinco personas.
Se debe entregar el informe en formato pdf y código fuente en (.zip) en el aula virtual de la materia.
El lenguaje de implementación es libre. Recomendamos utilizar C, C++ o Python. Sin embargo si se desea utilizar algún otro, se debe pactar con los docentes.
Incluir en el informe los requisitos y procedimientos para su compilación y ejecución. La ausencia de esta información no permite probar el trabajo y deberá ser re-entregado con esta información.
El informe debe presentar carátula con el nombre del grupo, datos de los integrantes y y fecha de entrega. Debe incluir número de hoja en cada página. No debe superar las 20 páginas + carátula + índice + referencias.
Debe entregar en el informe las fuentes consultadas en una sección de referencias.
En caso de re-entrega, entregar luego del informe original un apartado con las correcciones realizadas

Parte 1: Maximizando la ganancia del proyecto.

Un proyecto está compuesto por un conjunto de tareas a realizar. Cada tarea puede tener un conjunto de otras que se deben realizar previamente para poder comenzarla. Tenemos personal disponible que solo nos permite hacer una tarea por vez. La ganancia de cada tarea es variable según la cantidad de tareas que ya se realizaron anteriormente. Tenemos conocimiento de la ganancia de cada tarea por cada orden posible de ejecución (independientemente de la duración de cada tarea que es un dato que no afecta al resultado. Si lo considera puede suponer que todas las tareas duran exactamente 1 semana).

Nos solicitan que definamos el orden de todas las tareas para que se obtenga la mayor ganancia posible y a su vez se cumplan las precedencias.

Se pide:

Explique cómo resolvería el problema utilizando generar y probar. ¿Cuál sería la complejidad?
Proponga y explique una solución del problema mediante Branch and Bound (B&B).
Brinde pseudocódigo y estructuras de datos a utilizar para B&B.
Realice el análisis de complejidad temporal y espacial para B&B.
Brinde un ejemplo simple paso a paso del funcionamiento de su solución para B&B.
Programe su propuesta de B&B.
Determine si su programa tiene la misma complejidad que su propuesta teórica.

Para cada una de las partes utilizar la terminología correspondiente.

Formato de los archivos:

El programa debe recibir por parámetro un archivo con las tareas y otro con las ganancias. Ejemplo:

python proyecto.py tareas.txt ganancias.txt

El archivo de tareas corresponde a un archivo de texto donde cada línea corresponde a una tarea del proyecto. Está definido por un código numérico separado incremental, luego su nombre y las tareas precedentes que deben realizarse antes de esta. Cada uno de estos valores separados por coma. Ejemplo:

1,Tarea A 
2,Tarea B,1
3,Tarea C
4,Tarea D,2
5,Tarea E,2,3
6,Tarea F
7,Tarea G,5

El archivo de ganancias corresponde a un archivo de texto donde cada línea corresponde a una tarea definida por su código numérico. Luego separado por comas, la ganancia a obtener según la semana en la que se realiza. Ejemplo:

1,10,5,8,2,4,6,6
2,12,12,10,5,4,7,9
3,1,5,8,9,9,10,12
4,4,5,2,8,15,20,10
5,12,12,10,5,4,7,9
6,1,2,3,4,3,2,1
7,30,10,12,5,15,10,5

Debe resolver el problema y retornar por pantalla la solución. Primero el valor total de ganancia obtenido y luego el orden de las tareas a realizar con la ganancia obtenida por ella.

Parte 2: El costo del mantenimiento

En una red global existen un conjunto de servidores conectados mediante conexiones punto a punto. No todos los servidores están conectados entre sí, pero la comunicación se puede realizar pasando por servidores intermedios. Cada conexión tiene un patrocinador que paga un costo anual por ella. Operativamente la red tiene un costo elevado de mantenimiento relacionado con el número de conexiones. Los administradores desean conocer al mayor número de conexiones que se pueden eliminar, manteniendo la conectividad entre todos los servidores, minimizando la pérdida por patrocinio.

Se pide:

Determinar y explicar cómo se resolvería este problema utilizando la metodología greedy.
Brinde pseudocódigo y estructuras de datos a utilizar.
De un ejemplo paso a paso. ¿Qué complejidad temporal y espacial tiene la solución?
Justifique por qué corresponde su propuesta a la metodología greedy.
Demuestre que su solución es óptima.

Parte 3: Los planos de las piezas

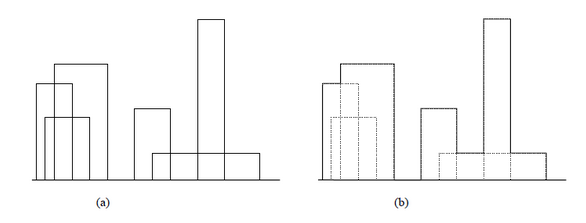
Para la elaboración de ciertas piezas se suelen realizar planos con vistas frontales y laterales de ellas. Las piezas están conformadas por diferentes partes. Cada parte tiene forma rectangular representado por rectángulos mediante la tripla (izquierda, altura, derecha). Izquierda y derecha corresponden al eje X y tienen valores positivos. La altura es con respecto al eje Y. También únicamente puede ser un valor cero o positivo. Para generar el plano se cuenta con el listado de las partes sin un orden específico y sus coordenadas en el plano. Por ejemplo:

Pieza 1: (1, 11, 5), (2, 6, 7), (3, 13, 9), (12, 7, 16) , (14, 3, 25), (19,18,22)  

Una parte del proceso requiere construir el contorno de la pieza representado como una lista de coordenadas “x” y sus alturas. Para el ejemplo anterior:

Contorno: (1,11),(3,13),(9,0),(12,7),(16,3),(19,18),(22,3),(25,0)

La siguiente imagen muestra las partes (a) y el contorno a generar (b):

pieza

Se pide:

Presentar un algoritmo que lo resuelva utilizando división y conquista.
Mostrar la relación de recurrencia
Presentar pseudocódigo
Analice la complejidad del algoritmo utilizando el teorema maestro y desenrollando la recurrencia
Brindar un ejemplo de funcionamiento
Programe su solución
Analice si la complejidad de su programa es equivalente a la expuesta en el punto 4

Formato de los archivos:

El programa debe recibir por parámetro un archivo con las partes de la pieza. Ejemplo:

python contorno.py partes.txt

El archivo de partes corresponde a un archivo de texto donde cada línea corresponde a una parte. Está definido por la tripla separados por coma.

Ejemplo:

1,11,5
2,6,7
3,13,9
12, 7,16
14,3,25
19,18,22

Debe resolver el problema y retornar por pantalla el contorno.