Trabajo Práctico n.º 3

Teoría de Algoritmos 1 - 2c 2020 Trabajo Práctico 3

Lineamientos básicos

• El trabajo se realizará en grupos de cuatro personas (excepcionalmente de tres o cinco).

• Se debe entregar el informe en formato pdf en el aula virtual de la materia.

• El informe debe presentar carátula con el nombre del grupo y número de hoja cada página.

Parte 1: Un escape lógico

Un nivel de un videojuego “escape room” consiste en un conjunto de salas contiguas. Todas las salas son iguales, excepto la primera y la última. Las salas intermedias tienen 2 sets de 3 puertas cada una. El primer trío conduce a la habitación anterior. Y el segundo trío la habitación siguiente. La particularidad de estas puertas es que son de 1 solo sentido. Dependen de una palanca que puede permitir únicamente entrar o salir (pero no las dos).

La última sala tiene un cofre con una llave que abre la puerta de salida de la primera habitación. En la primera habitación se encuentra un panel con un conjunto de palancas de 2 posiciones y un diagrama que muestra qué puertas están controladas por cada palanca. Una puerta sólo está controlada por una palanca. Pero una palanca puede controlar 1 o más puertas. Otra particularidad de este ingenio es que una misma palanca puede hacer que una puerta permita acceder a cuartos siguientes y otra puerta a cuartos anteriores.

Se desea encontrar un configuración de palancas de tal manera que se pueda acceder a la sala del cofre, retirar la llave y luego regresar a la sala inicial para escapar por la puerta.

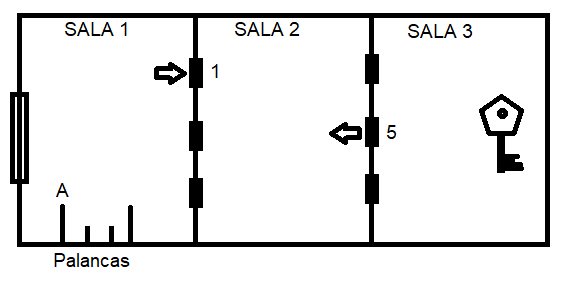
Ejemplo: Activar la palanca A, permite ingresar desde la puerta 1 de la “sala 1” a la “sala 2”. Además permite regresar de la “sala 3” a la “sala 2”. Si se desactiva la palanca se invierten los sentidos de las puertas.

Se pide:

1. Demostrar que es un problema NP-Completo

HINT 1: Este problema puede verse como una instancia de Not-All-Equal 3 Satisfiability (NAE-3SAT). Es similar a SAT, pero se requiere que en cada cláusula contenga al menos un literal en TRUE y al menos un literal en FALSE. (No asumir que NAE-3SAT es NP-C: demostrarlo!)

HINT 2: Utilice 3 SAT u otra variante de SAT a su gusto para la demostración

Parte 2: Un problema de agrupamiento.

Análisis de grupos o agrupamiento es la tarea de agrupar un conjunto de objetos de tal manera que los miembros del mismo grupo sean más similares, en algún sentido u otro.

Un investigador acude a nosotros para que le ayudemos a crear un método de agrupamiento. Propone representar a los objetos y sus distancias como un grafo ponderado. Por sus anteriores trabajos conoce el problema de corte mínimo - flujo máximo. Sabe que existen algoritmos que lo resuelven de forma eficiente. Nos propone que trabajemos en conjunto para encontrar el corte máximo y con eso construir la separación de los conjuntos.

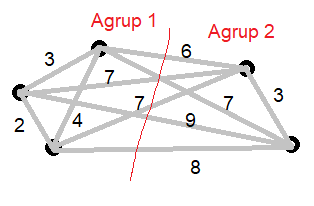
Se solicita:

1. Demostrar que su planteo es NP-Completo

2. ¿Dada la demostración anterior, se puede afirmar que el problema de clustering es NP-Completo?

HINT 1: El problema es conocido como MAX-CUT

HINT 2: Puede ayudarse para la resolución utilizando NAE-3SAT

Parte 3: Un poco de teoría

1. Defina y explique qué es una reducción polinomial y para qué se utiliza.

2. Explique detalladamente el problema “P =? NP”

3. Tenemos un problema A, un problema B y una caja negra NA y NB que resuelven el problema A y B respectivamente. Sabiendo que B es P

   1. Qué podemos decir de A si utilizamos NA para resolver el problema B (asumimos que la reducción realizada para adaptar el problema B al problema A es polinomial)

   2. Qué podemos decir de A si utilizamos NB para resolver el problema A (asumimos que la reducción realizada para adaptar el problema A al problema B es polinomial)

   3. ¿Qué pasa con los puntos anteriores si no conocemos la complejidad de B, pero sabemos que A es NP?