Trabajo Práctico n.º 1

Teoría de Algoritmos 1 - 2c 2020 Trabajo Práctico 1

Lineamientos básicos

El trabajo se realizará en grupos de cuatro personas (excepcionalmente de tres o cinco).
Se debe entregar el informe en formato pdf y código fuente en (.zip) en el aula virtual de la materia.
El lenguaje de implementación es libre. Recomendamos utilizar C, C++ o Python. Sin embargo si se desea utilizar algún otro, se debe pactar con los docentes.
Incluir en el informe los requisitos y procedimientos para su compilación y ejecución. La ausencia de esta información no permite probar el trabajo y deberá ser re-entregado con esta información.
El informe debe presentar carátula con el nombre del grupo y número de hoja cada página.

Parte 1: La exposición de arte

Un importante museo nacional tiene “n” piezas de arte en diferentes bóvedas de seguridad (1 pieza por bóveda inicialmente). Se ha programado una exposición especial que requiere que esas n piezas se reúnan para luego ser transportadas al lugar designado. Para la movilización se ha contratado un seguro que cobra un valor por cada vez que una pieza corre riesgo de robo (la bóveda que la contiene se abre). Cada pieza fue tasada con un valor determinado. Cuando se realiza un traslado hay 2 bóvedas involucradas. Se abren tanto la bóveda de origen como la de destino. Por lo tanto se debe pagar al seguro los valores de los que están almacenados en ambas bóvedas.

Deseamos determinar qué traslados realizar de forma de lograr unificar en una sola bóveda todos las piezas abonando la menor cantidad de plata a la aseguradora

Ejemplo:

Si tengo 4 piezas con sus respectivos valores en 4 bóvedas. A: p1=5 B: p2=4 C: p3=2 D: p4=6
Puede realizar los siguientes traslados
A (p1) → B (p2) : pago 5+4=9 (ahora en B tengo p1 y p2)
C (p3) → B (p1,p2): pago 2+9=11 (ahora en B tengo p1, p2 y p3)
D (p4) → B(p1, p2, p3): pago: 6+11=17 (ahora en B tengo todas las piezas)
Pago en total: 9+11+17=37 
También se puede trasladar de la siguiente manera
A (p1) → B (p2) : pago 5+4=9 (ahora en B tengo p1 y p2)
C (p3) → D (p4): pago 2+6=8 (ahora en D tengo p3 y p4)
B (p1, p2) → D (p3, p4): pago: 9+8=17 (ahora en D tengo todas las piezas)
Pago en total: 9+8+17=34 

Se pide:

Proponer una solución greedy que solucione el problema (y que sea óptimo)
Determinar la complejidad temporal y espacial del problema
Demostrar que la solución es óptima
Programar la solución
Analizar justificando si la complejidad temporal y espacial de lo programado se condice con la obtenida en el punto 2

Formato de los archivos:

Para la ejecución del programa se debe obtener las piezas de un archivo de texto que tenga en una línea separado por comas el valor tasado de cada una de las piezas (sin espacios). Ejemplo: 1,8,3,6,3

El programa debe recibir por parámetro la cantidad de piezas y el path al archivo con las valoraciones

Debe imprimir por pantalla los traslados y el costo acumulado de forma similar a la mostrada en los ejemplos

Parte 2: El contorno de la ciudad en un videojuego.

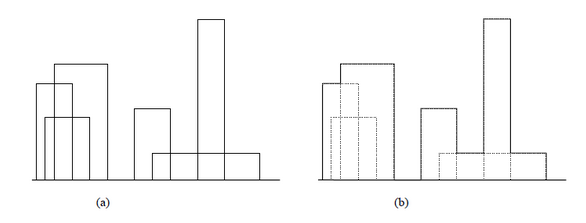
Para la elaboración de un juego se desea construir un cielo nocturno de una ciudad donde se vea el contorno de los edificios en el horizonte. Cada edificio “ei“ está representado por rectángulos mediante la tripla (izquierda, altura, derecha). Dónde “izquierda” corresponde a la coordenada x menor, “derecha” la coordenada x mayor y altura la coordenada y. Todos los edificios inician en la coordenada 0 de y. Se cuenta con una lista de N edificios que llegan sin un criterio de orden específico. Se desea emitir como resultado el contorno representado como una lista de coordenadas “x” y sus alturas.

Ejemplo:

Lista de edificios: (1, 11, 5), (2, 6, 7), (3, 13, 9), (12, 7, 16) , (14, 3, 25), (19,18,22) Contorno: (1,11),(3,13),(9,0),(12,7),(16,3),(19,18),(22,3),(25,0)

Skyline

Se pide:

Presentar un algoritmo utilizando división y conquista que dado el listado de edificios retorne como resultado el contorno de la ciudad.
Indicar relación de recurrencia
Analizar complejidad algorítmica (espacial y temporal)