Trabajo Práctico n.º 3

Teoría de Algoritmos 1 - 2c 2019 Trabajo Práctico 3

Lineamientos básicos

• El trabajo se realizará en grupos de cuatro personas (excepcionalmente de tres).

• La fecha de entrega es Miércoles 23 de Octubre. Se debe entregar en el horario de clase en papel (informe), más una entrega en digital de código (.zip) e informe (.pdf) a la clase de Google ClassRoom de la materia.

• El lenguaje de implementación es libre. Recomendamos utilizar C, C++ o Python. Sin embargo si se desea utilizar algún otro, se debe pactar con los docentes.

• Incluir en el informe los requisitos y procedimientos para su compilación y ejecución. La ausencia de esta información no permite probar el trabajo y deberá ser re-entregado con esta información.

• El informe debe presentar carátula con el nombre del grupo y número de hoja cada página

Parte 1: Rectangulo contenedor

Un polígono es convexo si al prolongar cualquiera de sus lados queda completamente en uno de los semiplanos que determina tal recta. Los polígonos convexos tienen propiedades que los hacen útiles en la resolución de problemas de geometría, geometría computacional e informática gráfica.

Se cuenta con un conjunto ordenado de puntos en el plano que representan los vértices de un polígono convexo. Se desea construir un algoritmo que retorne el mínimo rectángulo que contiene a la figura representada.

Como solución inicial nos sugieren recorrer todos los puntos y encontrar los 4 puntos extremos (aquellos que tienen las mayores y menores coordenados x e y. Una vez obtenidos con ellos delimitar el rectángulo.

Por otro lado, alguien nos anima a buscar una solución utilizando el paradigma de división y conquista.

Se pide:

1. Dar y explicar el pseudocódigo de la solución inicial.
2. Dar y explicar el pseudocódigo de la solución utilizando división y conquista.
3. Calcule la complejidad temporal y espacial de las soluciones dadas en el punto anterior.
4. Indique qué pasaría si el polígono no fuese convexo para ambas soluciones. Ejemplifique.
5. Analice cuántos vértices debe tener el polígono para que una solución sea preferible a la otra.
6. Programe las soluciones

Interface de los programas:

El programa para calcular el rectángulo tiene que recibir 2 parámetros:

• path del archivo donde están los vertices del poligono
• Método a utilizar para el cálculo: “inicial” (para solución inicial) o “dyc” para solucion y conquista

La salida tiene que ser un archivo llamado “rectangulo.txt” que contenga una linea por cada uno de los vertices del rectangulo. Ejemplo:

10,10
10,25
20,25
20,10

El archivo que contiene los vértices del polígono tendrá la sucesión de puntos que lo conforma. Cada punto estará en una línea. Con las coordenadas x e y separadas por coma.

Parte 2: Acomodando cajas

Un empresario dueño de un depósito automatizado nos pide que construyamos un algoritmo que permite trasladar una caja de almacenamiento de dimensiones standard de una ubicación inicial a una final determinada. La caja es un prisma rectangular que mide 2 de alto x 1 de ancho x 1 de largo. Las máquinas que trasladan la misma solo la puedan hacer girar en el piso (en cualquiera de sus ejes). Podemos considerar el depósito como una grilla de “n” filas x “m” columnas (con n y m valores enteros). Cada celda es de 1x1 metro. Algunas de las celdas están ocupadas por otras cajas que no podemos trasladar. La caja se encuentra inicialmente parada.

El algoritmo a construir debe utilizar programación dinámica. Tiene que determinar si es posible el traslado y si lo es, cual es el recorrido de menor cantidad de rotaciones. Además mostrar cuales son esas rotaciones.

En la siguiente imágen se muestra el movimiento posible de una caja de una posición inicial a una final.

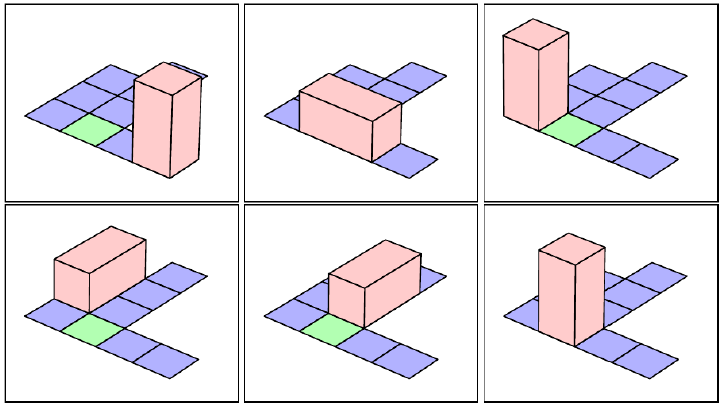
Se debe:

1. Explicar DETALLADAMENTE la solución propuesta. Presente pseudocódigo. Incluya relación de recurrencia.
2. Determine complejidad temporal y espacial de su solución.
3. Presente DOS ejemplos en forma detallada donde encuentra solución (realice un paso a paso de su algoritmo).
4. Presente UN ejemplo en forma detallada donde no se encuentra solución (realice un paso a paso de su algoritmo).

Parte 3: Análisis de un paper…

(Este ejercicio es “yapa” y no obligatorio)

Dentro de la industria de los videojuegos, los algoritmos de detección de colisiones son fundamentales (algunos ejemplos: Un automóvil que choca con otro en una carrera o una persona que recorre un bosque lleno de árboles y piedras). Es importante que este proceso sea rápido y exacto.

El paper “Fast detection of polyhedral intersection” (1983) publicado por Dobkin y Kirkpatrick ( https://www.cs.jhu.edu/~misha/Spring16/Dobkin83.pdf ) propone mediante el paradigma de “División y conquista” una solución para 2D y 3D.

Se pide:

1. Leer el paper y explicar cómo funciona el método en 2D.
2. Dar pseudocódigo de la solución y explicar su complejidad
3. Dar 2 ejemplos completos de funcionamiento (1 con y otro sin colisión)