Trabajo Práctico n.º 2

Teoría de Algoritmos 1 - 2c 2018 Trabajo Práctico 2

Lineamientos básicos

• El trabajo se realizará en grupos de cuatro personas (excepcionalmente de tres).

• La fecha de entrega es el lunes 22 de octubre de 2018. Se debe entregar en el horario de clase en papel (informe), más una entrega en digital de código (.zip) e informe (.pdf) al correo de entregas del curso: tps.7529rw@gmail.com y a la clase de Google ClassRom de la materia.

• El lenguaje de implementación es libre, pero se debe comunicar por correo en caso de no ser uno de: C, C++, Python, Java, JavaScript, Ruby, Go, Rust, Swift, Scala, Haskell, OCaml, Clojure, D, Lua, Elixir.

• Incluir en el informe los requisitos y procedimientos para su compilación y ejecución.

Parte 2: El robot y el camino seguro

Un robot debe llegar desde el punto en el que se encuentra a un destino determinado. Disponemos de un mapa que contiene un conjunto de puntos seguros (El punto inicial y el final son puntos seguros). Sabemos que existen accidentes geográficos donde el robot puede quedar atrapado. Estos accidentes se encuentran dentro de la envoltura convexa que contienen a los puntos seguros (aclaración: los puntos de inicio y finalizacion pertenecen a la envoltura convexa).

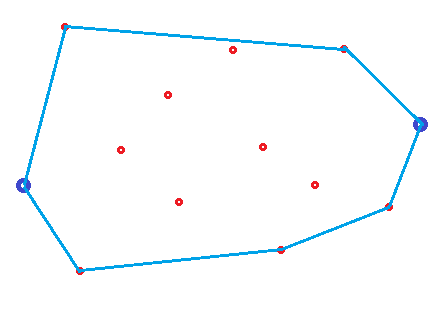
El objetivo final es, dados un input que contiene los puntos de origen, final y seguros, determinar el menor camino seguro posible. Para eso calcular la envoltura convexa. Los dos caminos posibles utilizando como ruta la envoltura. La selección del menor camino utilizando la distancia euclídea.

Se solicita:

Resolver el problema utilizando diferentes algoritmos para calcular la envoltura convexa

• Fuerza bruta
• Graham scan
• Un método de división y conquista.

Para cada algoritmo se solicita:

1. Explicar el método, presentar el pseudocódigo y las estructuras a utilizar.
2. Calcular y explicar la complejidad de su algoritmo (tiempo y espacio)
3. Programar la solución.
4. Explique y analice la reducción polinomial realizada para el problema planteado. Podemos afirmar que nuestro problema es P (desarrolle)?

Información adicional:

Utilizar como entrada un archivo de texto con el siguiente formato:

• Por cada línea dos números representando las coordenadas X e Y de puntos seguros separados por un espacio (números enteros).
• La primera línea corresponde al punto de origen
• La segunda línea corresponde al punto de destino

La salida debe ser mostrada en pantalla con el siguiente formato:

Camino 1: Longitud [poner longitud del camino]
Recorrido: [mostrar el x,y de cada punto iniciando desde origen y pasando en forma ordenada por los puntos seguros hasta el punto de destino]

Camino 2: Longitud [poner longitud del camino]
Recorrido: [mostrar el x,y de cada punto iniciando desde origen y pasando en forma ordenada por los puntos seguros hasta el punto de destino]

Camino seleccionado: [1 o 2]

El programa debe recibir por parámetro el nombre del archivo con los puntos y el tipo de algoritmo a utilizar (F: Fuerza bruta, G: Graham scan, D: División y conquista)

Parte 2: Una variante de SAT

2SAT o (2-satisfiability) es un caso particular del problema SAT. En este caso las cláusulas lógicas comprenden únicamente 2 variables.

1. Definir una reducción de un problema de 2SAT a un problema de 3SAT
2. Investigar y responder justificando la validez de la siguiente afirmación: “Es posible resolver una instancia de 2SAT utilizando una reducción polinomial a un problema de grafos, a su vez resoluble en tiempo polinomial”
3. Analice la implicancia de los puntos 1 y 2 a la luz del problema de P=NP

Parte 3: El problema de los pasantes

Un grupo de pasantes de un museo de antropología se han metido en un problema. Sin querer han tirado algunos cajas y mezclado colecciones de X objetos recolectados en dos excavaciones. Dado su inexperiencia, su apuro y la similitud de las piezas tienen como idea comparar de a pares para intentar volver a separarlos. Por cada par de toman definen si pertenece a la misma colección, diferente o si no están seguros.

1. Ayude a los pasantes a determinar mediante un algoritmo eficiente si es posible separar las colecciones basándose en sus clasificaciones. (ayuda: pruebe una solución utilizando grafos)
2. Determine el orden de complejidad del algoritmo propuesto.
3. Ejemplifique el funcionamiento de su algoritmo con un caso donde se pueda clasificar y otro en el que no.