Grafos: Usos, implementaciones, recorridos, aplicaciones

Contenidos

  1. Ejercicio resuelto
    1. Solución
  2. Ejercicios propuestos

Ejercicio resuelto

Implementar un algoritmo que, dado un grafo no dirigido, nos devuelva un ciclo dentro del mismo, si es que los tiene. Indicar el orden del algoritmo.

Solución

Antes que nada, debemos entender que el ejercicio en sí es el mismo, se trate de un grafo dirigido o uno no dirigido. La única diferencia se encuentra en que un ciclo por definción necesita contar con al menos dos aristas. Esta definición en sí no nos importaría mucho en el caso de un grafo dirigido, pero si en el de uno no dirigido. Si no lo tuviéramos en cuenta, todo grafo no dirigido, con al menos una arista, va a tener un ciclo, lo cual no es cierto.

Para resolver este problema, podemos pensar en simplemente recorrer el grafo no dirigido, sea con un recorrido BFS o DFS. Una vez que nos topemos con un vértice ya visitado, ahí tenemos un posible ciclo. Esto es, si estoy viendo los adyacentes a un vértice dado, y dicho vértice está visitado, uno se apresuraría a decir que ahí se cierra un ciclo. Esto es cierto, salvo un caso: que dicho vértice visitado sea el antecesor a nuestro vértice en el recorrido (BFS o DFS). Recordar que se trata de un grafo no dirigido, por ende si v tiene de adyacente a w, entonces también vale la recíproca, y no por ello se crea un ciclo. El problema se da con la arista de la que vengo. Básicamente, deberíamos obviar al vértice del que vengo en el recorrido, que justamente es el padre. Si nosotros ya tenemos que padre[W] = V, entonces simplemente tenemos que saltearnos a V cuando veamos a los adyacentes ya visitados.

Lo resolvemos con ambos recorridos. Por DFS:

def obtener_ciclo_dfs(grafo):
  visitados = {}
  padre = {}
  for v in grafo:
    if v not in visitados:
      ciclo = dfs_ciclo(grafo, v, visitados, padre)
      if ciclo is not None:
        return ciclo
  return None

def dfs_ciclo(grafo, v, visitados, padre):
  visitados[v] = True
  for w in grafo.adyacentes(v):
    if w in visitados:
      # Si w fue visitado y es padre de v, entonces es la arista de donde
      # vengo (no es ciclo).
      # Si no es su padre, esta arista (v, w) cierra un ciclo que empieza
      # en w.
      if w != padre[v]:
        return reconstruir_ciclo(padre, w, v)
    else:
      padre[w] = v
      ciclo = dfs_ciclo(grafo, w, visitados, padre)
      if ciclo is not None:
        return ciclo

  # Si llegamos hasta acá es porque no encontramos ningún ciclo.
  return None

def reconstruir_ciclo(padre, inicio, fin):
  v = fin
  camino = []
  while v != inicio:
    camino.append(v)
    v = padre[v]
  camino.append(inicio)
  return camino.invertir()

Por BFS, la solución sería similar, pero tenemos que tener noción de la distancia/orden. Esto es porque podríamos terminar sin encontrar un ciclo correctamente. Por ejemplo, si tenemos un grafo con 4 vértices en forma de cuadrado (aristas A-B, B-C, C-D, D-A), y empezamos a hacer el recorrido desde A, eventualmente en el BFS vamos a encontrar el ciclo (ej, al ver desde C para ir a D), pero al reconstruir el camino probablemente falle. Es necesario modificar el algoritmo para reconstruir el camino:

def obtener_ciclo_bfs(grafo):
  visitados = {}
  for v in grafo:
    if v not in visitados:
      ciclo = bfs_ciclo(grafo, v, visitados)
      if ciclo is not None:
        return ciclo
  return None

def bfs_ciclo(grafo, v, visitados):
  q = Cola()
  q.encolar(v)
  visitados[v] = True
  padre = {}  # Para poder reconstruir el ciclo
  orden = {}
  padre[v] = None
  orden[v] = 0

  while not q.esta_vacia():
    v = q.desencolar()
    for w in grafo.adyacentes(v):
      if w in visitados:
        # Si w fue visitado y es padre de v, entonces es la arista
        # de donde vengo (no es ciclo).
        # Si no es su padre, esta arista (v, w) cierra un ciclo que
        # empieza en w.
        if w != padre[v]:
          return reconstruir_ciclo(padre, orden, w, v)
      else:
        q.encolar(w)
        visitados[v] = True
        padre[w] = v
        orden[w] = orden[v] + 1

  # Si llegamos hasta acá es porque no encontramos ningún ciclo.
  return None
  
def reconstruir_camino(padre, orden, v1, v2):
    ciclo = []
    if orden[v1] != orden[v2]: # no puede haber más que 1 de diferencia
        if orden[v1] > orden[v2]:
             ciclo.append(v1)
             v1 = padre[v1]
        else:
             ciclo.append(v2)
             v2 = padre[v2]
    while v1 != v2:
        ciclo.append(v1)
        ciclo.append(v2)
        v1 = padre[v1]
        v2 = padre[v2]
    ciclo.append(v1)
    return ciclo

Ahora bien, para ver el orden, podemos ver que en el caso feliz, vamos a encontrar un ciclo muy rapido. Pero claramente eso no nos cambia mucho. Pensemos el caso de, a lo sumo, encontrar el ciclo muy tarde en el recorrido (también veremos el caso de no haber ciclo). En ese caso, en cualquiera de los dos recorridos vamos a pasar por cada vértice una vez, y solo una vez (a fin de cuentas, no volvemos a estar sobre un vértice ya visitado). Por cada vértice vemos sus aristas. Recordar que es muy importante no caer en la tentación de decir que entonces el algoritmo es \(\mathcal{O}(V \times E)\), porque si bien es cierto, es una muy mala cota. Por cada vértice pasamos por sus aristas, que distan de ser las totales del grafo. Si por cada vértice vemos sus aristas (y no las de todo el grafo), en total estamos viendo todas las aristas del grafo, dos veces (una por cada extremo). Entonces, el orden será \(\mathcal{O}(V + 2 E) = \mathcal{O}(V + E)\). Todo esto, considerando que la implementación es con listas de adyacencias (implementadas con diccionarios, o bien siendo los vértices valores numéricos para indexar en un arreglo). Si fuera otra la implementación, obtener los adyacentes a un vértice dado nos costará más (\(\mathcal{O}(V)\), en el caso de una matriz de adyacencia, u \(\mathcal{O}(E)\) en el caso de una matriz de incidencia).

Haciendo un poco más de análisis: ¿es acaso el caso de no tener ciclos nuestro peor caso? Supongamos que el grafo es conexo, por simplifcación. Si el grafo no tiene ciclos, y es conexo, necesariamente se trata de un árbol. Para este caso, \(|E| = |V| - 1\), por ende nuestro orden a fin de cuentas terminaría siendo \(\mathcal{O}(V)\). ¿Esto implica que entonces nuestro algoritmo es en realidad \(\mathcal{O}(V)\)? No, significa que ese, que a priori podíamos pensar que era nuestro peor caso, en realidad no lo es. Nuestro peor caso implica que haya un ciclo, pero tener la mala suerte de tardar en encontrarlo. Ya sea porque el vértice en el que se empieza el recorrido está lejos del ciclo, o por el orden aleatorio de las cosas.

¿Cuáles serían las diferencias si en vez de trabajar con un grafo no dirigido, lo hiciéramos sobre un grafo dirigido? Notar que la solución no debería ser demasiado distinta a estas propuestas, pero tienen sus pequeñas diferencias que dejamos para resolver en los ejercicios propuestos.

Ejercicios propuestos

  1. (★) a. Dibujar un grafo no dirigido que:
    • Tenga 6 vértices
    • Tenga un ciclo que incluya 4 de dichos vértices
    • Sea conexo
    • Haya un vértice de grado 1
    • Haya un vértice de grado 4

    b. Escribir la representación de matriz de incidencia y matriz de adyacencia del grafo resultante del punto anterior.

  2. (★) a. Dibujar un grafo dirigido que:
    • Tenga 7 vértices
    • Tenga un ciclo que incluya 3 de dichos vértices
    • Tenga un ciclo que incluya 2 de dichos vértices
    • Haya un vértice de grado de entrada 0
    • Haya un vértice de grado de salida 4

    b. Escribir la representación de matriz de incidencia y matriz de adyacencia del grafo resultante del punto anterior.

  3. (★) Implementar una función que determine el:

    a. El grado de todos los vértices de un grafo no dirigido.

    b. El grado de salida de todos los vértices de un grafo dirigido.

    c. El grado de entrada de todos los vértices de un grafo dirigido.

  4. (★) Implementar un algoritmo que determine si un grafo no dirigido es conexo o no. Indicar la complejidad del algoritmo si el grafo está implementado con una matriz de adyacencia.

  5. (★★★) Implementar un algoritmo que, dado un grafo dirigido, nos devuelva un ciclo dentro del mismo, si es que lo tiene. Indicar el orden del algoritmo.

  6. (★★) Un árbol es un grafo no dirigido que cumple con las siguientes propiedades:

    a. \(\|E\| = \|V\| - 1\)

    b. Es acíclico

    c. Es conexo

    Por teorema, si un grafo cumple dos de estas tres condiciones, será árbol (y por consiguiente, cumplirá la tercera). Haciendo uso de ésto (y únicamente de ésto), se pide implementar una función que reciba un grafo no dirigido y determine si se trata de un árbol, o no. Indicar el orden de la función implementada.

  7. (★★) Proponer una función para calcular el grafo traspuesto \(G^T\) de un grafo dirigido G. El grafo traspuesto \(G^T\) posee los mismos vértices que G, pero con todas sus aristas invertidas (por cada arista (v, w) en G, existe una arista (w, v) en \(G^T\)). Indicar la complejidad para un grafo implementado con:

    a. lista de adyancencias

    b. matriz de adyacencias

  8. (★★★) La teoría de los 6 grados de separación dice que cualquiera en la Tierra puede estar conectado a cualquier otra persona del planeta a través de una cadena de conocidos que no tiene más de cinco intermediarios (conectando a ambas personas con solo seis enlaces). Suponiendo que se tiene un grafo G en el que cada vértice es una persona y cada arista conecta gente que se conoce (el grafo es no dirigido):

    a. Implementar un algoritmo para comprobar si se cumple tal teoría para todo el conjunto de personas representadas en el grafo G. Indicar el orden del algoritmo.

    b. Suponiendo que en el grafo G no habrán altas ni bajas de vértices, pero podrían haberla de aristas (la gente se va conociendo), explicar las ventajas y desventajas que tendría implementar al grafo G con una matriz de adyacencia.

  9. (★★★) Matías está en Barcelona y quiere recorrer un museo. Su idea es hacer un recorrido bastante lógico: empezar en una sala (al azar), luego ir a una adyacente a ésta, luego a una adyancente a la segunda (si no fue visitada aún), y así hasta recorrer todas las salas. Cuando no tiene más salas adyacentes para visitar (porque ya fueron todas visitadas), simplemente vuelve por donde vino buscando otras salas adyacentes. Teniendo un grafo no dirigido, que representa el mapa del museo (donde los vértices son salas, y las aristas (v, w) indican que las salas v y w se encuentran conectadas), implementar un algoritmo que nos devuelva una lista con un recorrido posible de la idea de Matías para visitar las salas del museo. Indicar el recorrido utilizado y el orden del algoritmo. Justificar.

  10. (★★) Escribir una función bool es_bipartito(grafo) que dado un grafo no dirigido devuelva true o false de acuerdo a si es bipartito o no. Indicar y justificar el orden del algoritmo. ¿Qué tipo de recorrido utiliza?

  11. (★★★) Implementar un algoritmo que reciba un grafo dirigido, un vértice V y un número N, y devuelva una lista con todos los vértices que se encuentren a exactamente N aristas de distancia del vértice V. Indicar el tipo de recorrido utilizado y el orden del algoritmo. Justificar.

  12. (★★) Implementar una función que permita determinar si un grafo puede ser no dirigido. Determinar el orden del algoritmo implementado.

  13. (★★) a. Dada la siguiente matriz de adyacencias, escribir la representación del grafo como una lista de adyacencias:

    |   | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | 0 | 7 | 5 | 0 | 3 | 8 |
| B | 7 | 0 | 0 | 0 | 1 | 3 |
| C | 5 | 0 | 0 | 5 | 3 | 2 |
| D | 0 | 0 | 5 | 0 | 2 | 0 |
| E | 3 | 1 | 3 | 2 | 0 | 0 |
| F | 8 | 3 | 2 | 0 | 0 | 0 |

    b. ¿Qué complejidad tiene hacer esta traducción?

    c. ¿Qué ventajas y desventajas encuentra en cada representación? Explicar teniendo en cuenta cuestiones de espacio y tiempo según las operaciones que admite un grafo y considerar que las listas de adyacencias es un diccionario de listas.

  14. (★★) Explicar las ventajas y desventajas de un grafo implementado con listas de adyacencia (lista de listas) por sobre una implementación de matriz de adyacencia, sabiendo que su densidad es \(\frac{|E|}{max\ |E|} > 0.75\) o superior.

  15. (★★★) Un autor decidió escribir un libro con varias tramas que se puede leer de forma no lineal. Es decir, por ejemplo, después del capítulo 1 puede leer el 2 o el 73; pero la historia no tiene sentido si se abordan estos últimos antes que el 1.

    Siendo un aficionado de la computación, el autor ahora necesita un orden para publicar su obra, y decidió modelar este problema como un grafo dirigido, en dónde los capítulos son los vértices y sus dependencias las aristas. Así existen, por ejemplo, las aristas (v1, v2) y (v1, v73).

    Escribir un algoritmo que devuelva un orden en el que se puede leer la historia sin obviar ningún capítulo. Indicar la complejidad del algoritmo.

  16. (★★) Implementar una función que reciba un grafo no dirigido y no pesado implementado con listas de adyacencia (diccionario de diccionarios) y devuelva una matriz que sea equivalente a la representación de matriz de adyacencia del mismo grafo. Indicar y justificar el orden del algoritmo implementado.

  17. (★★) Implementar una función que reciba un grafo no dirigido, y que compruebe la siguiente afirmación: “La cantidad de vértices de grado IMPAR es PAR”. Indicar y justificar el orden del algoritmo si el grafo está implementado como matriz de adyacencia.

  18. (★★★★) Dado un número inicial X se pueden realizar dos tipos de operaciones sobre el número:

    • Multiplicar por 2
    • Restarle 1.

    Implementar un algoritmo que encuentra la menor cantidad de operaciones a realizar para convertir el número X en el número Y, con tan solo las operaciones mencionadas arriba (podemos aplicarlas la cantidad de veces que querramos).

  19. (★★★★★) Se tiene un arreglo de palabras de un lenguaje alienigena. Dicho arreglo se encuentra ordenado para dicho idioma (no conocemos el orden de su abecedario). Implementar un algoritmo que reciba dicho arreglo y determine un orden posible para las letras del abecedario en dicho idioma. Por ejemplo: 
    {"caa", "acbd", "acba", "bac", "bad"} --> ['c', 'd', 'a', 'b']

  20. (★★) Implementar un algoritmo que reciba un grafo dirigido y nos devuelva la cantidad de componentes débilmente conexas de este. Indicar y justificar la complejidad del algoritmo implementado.

  21. (★★★) Contamos con un grafo dirigido que modela un ecosistema. En dicho grafo, cada vértice es una especie, y cada arista (v, w) indica que v es depredador natural de w. Considerando la horrible tendencia del ser humano por llevar a la extinción especies, algo que nos puede interesar es saber si existe alguna especie que, si llegara a desaparecer, rompería todo el ecosistema: quienes la depredan no tienen un sustituto (y, por ende, pueden desaparecer también) y/o quienes eran depredados por esta ya no tienen amenazas, por lo que crecerán descontroladamente. Implementar un algoritmo que reciba un grafo de dichas características y devuelva una lista de todas las especies que cumplan lo antes mencionado. Indicar y justificar la complejidad del algoritmo implementado.

  22. (★★★) Implementar una función que reciba un grafo no dirigido y determine si el mismo no tiene ciclos de una cantidad impar de vértices. Indicar y justificar la complejidad de la función.

  23. (★★★) El diámetro de una red es el máximo de las distancias mínimas entre todos los vértices de la misma. Implementar un algoritmo que permita obtener el diámetro de una red, para el caso de un grafo no dirigido y no pesado. Indicar el orden del algoritmo propuesto.

  24. (★★) a. Obtener una representación del camino mínimo desde el vértice A en el siguiente grafo (representado con una matriz de adyacencias), hacia todos los demás vértices, utilizando el algoritmo de Dijkstra:

    |   | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | 0 | 7 | 5 | 0 | 3 | 8 |
| B | 7 | 0 | 0 | 0 | 1 | 3 |
| C | 5 | 0 | 0 | 5 | 3 | 2 |
| D | 0 | 0 | 5 | 0 | 2 | 0 |
| E | 3 | 1 | 3 | 2 | 0 | 0 |
| F | 8 | 3 | 2 | 0 | 0 | 0 |

    b. ¿Qué condiciones debe cumplir el grafo para poder aplicar el algoritmo de Dijkstra? ¿Qué característica tiene el grafo si al finalizar la ejecución del algoritmo, uno o más vértices quedan a distancia infinita?

  25. (★★★) a. Obtener una representación del camino mínimo desde el vértice A en el siguiente grafo (representado con una matriz de adyacencias), hacia todos los demás vértices, utilizando el algoritmo de Bellman-Ford.

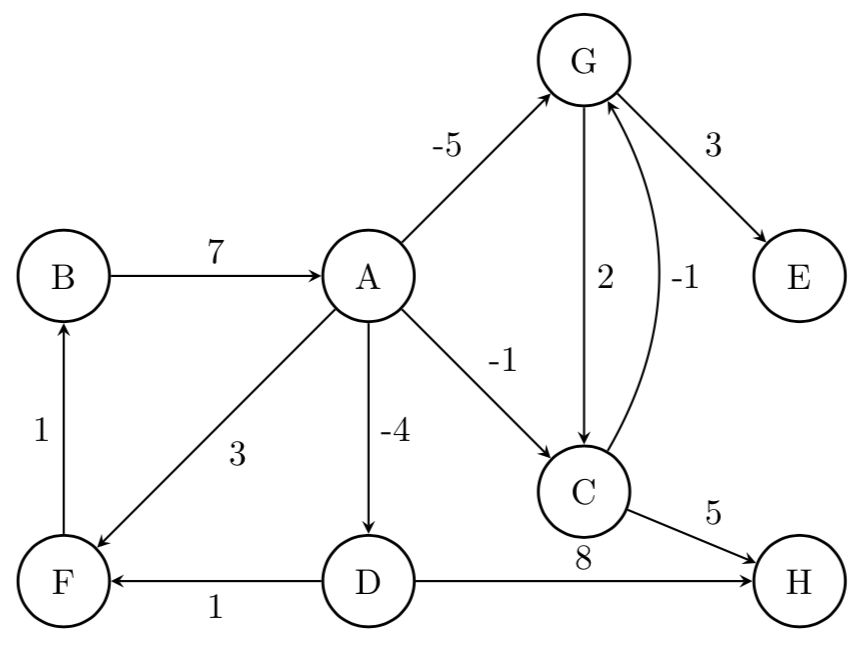
    grafo bf

    b. Volver a realizar, suponiendo que la arista de B a A ahora tiene un peso de 1.

  26. (★★) Obtener el Árbol de Tendido Mínimo del siguiente grafo:

    a. Utilizando el Algoritmo de Kruskal.

    b. Utilizando el Algoritmo de Prim.

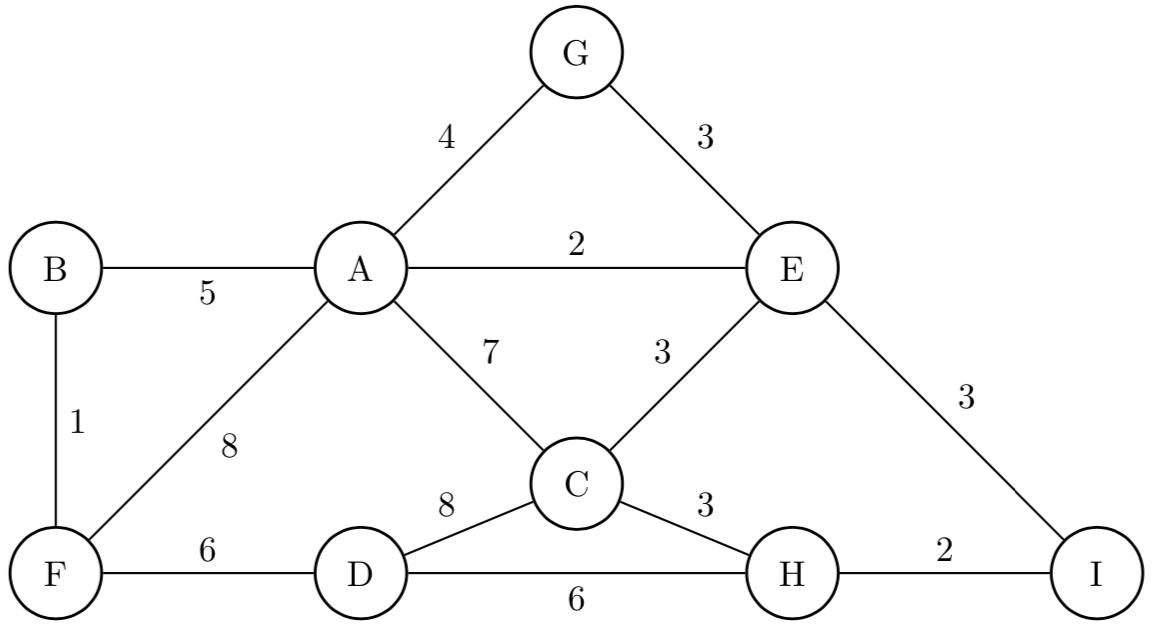
    grafo mst

  27. (★★★) Dadas las matrices de adyacencia M1, M2 y M3, responder las siguientes preguntas (recomendamos pasar los grafos a una representación visual para mayor facilidad):

    a. ¿Puede ser el grafo definido por M2 un árbol de tendido mínimo de M1? Justificar.

    b. Realizar un seguimiento de aplicar el algoritmo de Kruskal para obtener un árbol de tendido mínimo del grafo definido por M3.

    | M1 | A | B | C | D | E | F | G |
|----|---|---|---|---|---|---|---|
| A  | 0 | 3 | 4 | 0 | 0 | 0 | 0 |
| B  | 3 | 0 | 5 | 3 | 3 | 0 | 0 |
| C  | 4 | 5 | 0 | 2 | 0 | 0 | 6 |
| D  | 0 | 3 | 2 | 0 | 4 | 2 | 1 |
| E  | 0 | 3 | 0 | 4 | 0 | 6 | 0 |
| F  | 0 | 0 | 0 | 2 | 6 | 0 | 0 |
| G  | 0 | 0 | 6 | 1 | 0 | 0 | 0 |

| M2 | A | B | C | D | E | F | G |
|----|---|---|---|---|---|---|---|
| A  | 0 | 3 | 4 | 0 | 0 | 0 | 0 |
| B  | 3 | 0 | 0 | 0 | 3 | 0 | 0 |
| C  | 4 | 0 | 0 | 2 | 0 | 0 | 6 |
| D  | 0 | 0 | 2 | 0 | 0 | 2 | 0 |
| E  | 0 | 3 | 0 | 0 | 0 | 0 | 0 |
| F  | 0 | 0 | 0 | 2 | 0 | 0 | 0 |
| G  | 0 | 0 | 6 | 0 | 0 | 0 | 0 |

| M3 | A | B | C | D  | E  | F  | G  |
|----|---|---|---|----|----|----|----|
| A  | 0 | 6 | 0 | 4  | 0  | 0  | 0  |
| B  | 6 | 0 | 7 | 8  | 6  | 0  | 0  |
| C  | 0 | 7 | 0 | 0  | 4  | 0  | 0  |
| D  | 4 | 8 | 0 | 0  | 14 | 5  | 0  |
| E  | 0 | 6 | 4 | 14 | 0  | 7  | 8  |
| F  | 0 | 0 | 0 | 5  | 7  | 0  | 10 |
| G  | 0 | 0 | 0 | 0  | 8  | 10 | 0  |

  28. (★★) Analizar la complejidad del algoritmo de Prim según si el grafo está implementado con listas de adyacencia o matriz de adyacencia.

  29. (★★) Responder las siguientes preguntas, justificando la respuesta:

    a. Al aplicar sobre un grafo el algoritmo de Dijkstra para encontrar caminos mínimos desde un vértice \(v\) cualquiera, se obtiene un árbol definido por el diccionario de padres (que permite reconstruir dichos caminos mínimos). Dicho árbol, ¿es siempre de tendido mínimo?

    b. Al obtener un árbol de tendido mínimo de un grafo, se asegura que la suma de los pesos de las aristas sean mínimos. ¿Es posible utilizar el árbol de tendido mínimo para encontrar el camíno mínimo entre dos pares de vértices cualesquiera?

    c. Si un grafo es no pesado, ¿Se puede utilizar el Algoritmo de Dijkstra para obtener los caminos mínimos en dicho grafo?

  30. (★★★★) Se cuenta con un grafo en el que sus aristas tiene peso 1 o 2, únicamente. Implementar un algoritmo que permita obtener el camino mínimo de un vértice hacia todos los demás, en tiempo \(\mathcal{O}(V + E)\).

  31. (★★★★★) Implementar un algoritmo que, dado un grafo dirigido, un vértice \(s\) y otro \(t\) determine la cantidad mínima de aristas que deberían cambiar de sentido en el grafo para que exista un camino de \(s\) a \(t\).

  32. (★★★) Se tiene un Grafo no dirigido G, y un árbol de tendido mínimo T, de G. Se obtiene una de las aristas de G, que no se encuentra en T, y se le reduce el peso. Dar un algoritmo lineal que permita determinar el nuevo árbol de tendido mínimo T'(notar que T' podría ser igual a T). Justificar la complejidad del algoritmo.

  33. (★★★) Como todos sabemos, Taller de Programación I implica programar mucho. El equipo de Federico esta desarrollando un Age of Empires y le asignaron el modulo de movimientos. Dispone de un mapa, podríamos decir una grilla, donde se puede ver para cada celda su contenido (por ejemplo si está libre, si es agua, un árbol, etc). Fede tiene que implementar un algoritmo que, a partir de una unidad (por ejemplo un soldado), en una celda en especifico encuentre el camino a una celda objetivo. Considerar que entre celdas puede haber diferencia de alturas por lo que puede costarle mas (o menos) a una unidad ir de una celda a otra. Por supuesto que no puede ser cualquier camino, si no el que haga que la unidad llegue más rápido a su objetivo.

    a. Modelar el problema usando Grafos especificando de forma completa todos sus componentes.

    b. Implementar un algoritmo que a partir de una celda de origen y una de destino, retorne el camino que tiene que hacer la unidad, indicando y justificando la complejidad final.

  34. (★★★★) Grace, docente de un primer grado de un colegio primario, tiene como tarea armar la fila el acto del 9 de julio. Como no quiere que los chicos se distraigan, quiere que cada uno quede entre dos personas de las cuales no es amigo. Para eso dispone de un mapa de amistades donde se puede ver quién es amigo de quién.

    a. Modelar el problema usando Grafos especificando de forma completa todos sus componentes.

    b. Implementar un algoritmo que reciba como parametro el grafo del punto anterior y retorne una posible fila en formato de lista. Retornar lista vacia si no existe solución. Indicar y justificar la complejidad final.

    Pista: No pensar el ejercicio armando, inicialmente, la fila sino viendo como separar a cada uno de sus amigos. Resolución de este ejercicio aquí (coming soon).